Parametric and Nonparametric Estimation of Population Mean in Poisson-Xgamma Distribution with Applications to Count Data

Patarawan Sangnawakij

doi:10.59796/jcst.V15N2.2025.102

Authors

Patarawan Sangnawakij Department of Mathematics and Statistics, Faculty of Science and Technology, Thammasat University, Pathum Thani 12120, Thailand

DOI:

https://doi.org/10.59796/jcst.V15N2.2025.102

Keywords:

asymptotic theory, bootstrap, compounding discrete distribution, count data, overdispersion

Abstract

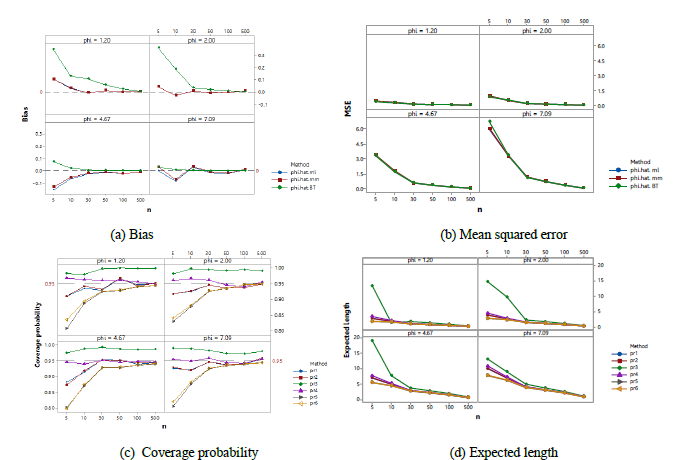
This study proposes new estimators and confidence intervals for the population mean of the Poisson-Xgamma distribution, which are useful for overdispersed count data analysis. We prove that the proposed estimators using maximum likelihood and method of moments estimation are consistent and establish the variance of the estimators. Moreover, the confidence intervals are constructed based on large-sample theory and bootstrap method. The former method utilizes the properties of the maximum likelihood and moment estimators, the likelihood ratio, and the asymptotic normality property of the log-transformed maximum likelihood estimator. Percentile bootstrap and bias-corrected and accelerated confidence intervals are considered. The performance of the estimators is investigated through simulations in terms of bias, mean squared error, coverage probability, and length of interval. According to the simulations, the log-transformed maximum likelihood estimation-based confidence interval for the mean provides excellent and better coverage rates than the other competitive methods. Furthermore, two real data sets are used to demonstrate our estimators and perform a comparison that supports the findings obtained from the simulation study.

References

Alghamdi, F. M., Ahsan-ul-Haq, M., Hussain, M. N. S., Hussam, E., Almetwally, E. M., Aljohani, H. M., ... & Yusuf, M. (2024). Discrete Poisson Quasi-XLindley distribution with mathematical properties, regression model, and data analysis. Journal of Radiation Research and Applied Sciences, 17(2), Article 100874. https://doi.org/10.1016/j.jrras.2024.100874

Altun, E., Cordeiro, G. M., & Ristic, M. M. (2022). An one-parameter compounding discrete distribution. Journal of Applied Statistics, 49(8), 1935-1956. https://doi.org/10.1080/02664763.2021.1884846

Böhning, D., Bunge, J., & Heijden, P. G. (Eds.). (2018). Capture-recapture methods for the social and medical sciences. Boca Raton: CRC Press.

Böhning, D., Sangnawakij, P., & Holling, H. (2022). Confidence interval estimation for the Mantel–Haenszel estimator of the risk ratio and risk difference in rare event meta-analysis with emphasis on the bootstrap. Journal of Statistical Computation and Simulation, 92(6), 1267-1291. https://doi.org/10.1080/00949655.2021.1991347

Casella, G., & Berger, R. (2002). Statistical inference. Duxbury Press.

Chernick, M. R., & LaBudde, R. A. (2011). An introduction to bootstrap methods with applications to R. John Wiley & Sons.

Conway, R. W., & Maxwell, W. L. (1962). A queueing model with state dependent service rates. Journal of Industrial Engineering, 12(2), 132-136.

Doganaksoy, N. (2021). A simplified formulation of likelihood ratio confidence intervals using a novel property. Technometrics, 63(1), 127-135. https://doi.org/10.1080/00401706.2020.1750488

Déniz, E. G. (2013). A new discrete distribution: Properties and applications in medical care. Journal of Applied Statistics, 40(12), 2760-2770. https://doi.org/10.1080/02664763.2013.827161

Efron, B. (1987). Better bootstrap confidence intervals. Journal of the American Statistical Association, 82(397), 171-185. https://doi.org/10.2307/2289144

Efron, B., & Narasimhan, B. (2020). The automatic construction of bootstrap confidence intervals. Journal of Computational and Graphical Statistics, 29(3), 608-619. https://doi.org/10.1080/10618600.2020.1714633

Efron, B., & Tibshirani, R. J. (1993). An introduction to the bootstrap. Chapman and Hall/CRC.

Gangopadhyay, A. K., Mondal, R., Lodhi, C., & Maiti, K. (2024). Bayesian inference on parameters and reliability characteristics for inverse Xgamma distribution under adaptive-general progressive Type-II censoring. Journal of Radiation Research and Applied Sciences, 17(2), 1-17. https://doi.org/10.1016/j.jrras.2024.100890

Ghalanos, A., & Theussl, S. (2015). General non-linear optimization. Retrieved July 2024, from https://cran.r-project.org/web/packages/Rsolnp/Rsolnp.pdf

Gschlöbl, S., & Czado, C. (2008). Modelling count data with overdispersion and spatial effects. Statistical Papers, 49, 531-552. https://doi.org/10.1007/s00362-006-0031-6

Hilbe, J. M. (2011). Negative binomial regression. Cambridge University Press.

Hilbe, J. M. (2017). The statistical analysis of count data. Culture and Education, 29(3), 409-460. https://doi.org/10.1080/11356405.2017.1368162

Huang, A. (2023). On arbitrarily underdispersed discrete distributions. American Statistical Association, 77(1), 29-34. https://doi.org/10.1080/00031305.2022.2106305

Hudson, D. J. (1971). Interval estimation from the likelihood function. Journal of the Royal Statistical Society Series B. 33(2), 256-262. https://www.jstor.org/stable/2985006

Imoto, T., Ng, C. M., Ong, S. H., & Chakraborty, S. (2017). A modified Conway-Maxwell-Poisson type binomial distribution and its applications. Communications in Statistics - Theory and Methods, 46(24), 12210-12225. https://doi.org/10.1080/03610926.2017.1291974

Kropko, J., & Harden, J. J. (2020). Beyond the hazard ratio: generating expected durations from the cox proportional hazards model. British Journal of Political Science, 50(1), 303-320. https://doi.org/10.1017/S000712341700045X

Meeker, W. Q., Escobar, L. A., & Pascual, F. G. (2021). Statistical methods for reliability data. John Wiley & Sons.

Mooney, C. Z., & Duval, R. D. (1993). Bootstrapping: A nonparametric approach to statistical inference. Sage Publications.

Oehlert, G. W. (1992). A note on the delta method. The American Statistician, 46(1), 27-29. https://doi.org/10.2307/2684406

Oseni, B. M., Makinde, O. S., & Adepetun, A. O. (2024). Dispersion insensitive truncated models for inflated count data with upper bound. Communications in Statistics-Simulation and Computation, 53(12), 5884-5898. https://doi.org/10.1080/03610918.2023.2202843

Perumean-Chaney, S. E., Morgan, C., McDowall, D., & Aban, I. (2013). Zero-inflated and overdispersed: what's one to do?. Journal of Statistical Computation and Simulation, 83(9), 1671-1683. https://doi.org/10.1080/00949655.2012.668550

R Core Team. (2024). R: A language and environment for statistical computing [Computer software]. R Foundation for Statistical Computing. https://www.r-project.org/

Sangnawakij, P. (2024). A Simple Profile Likelihood-based Confidence Interval for the Risk Ratio in Rare Events Meta-analysis. Thailand Statistician, 22(2), 312-327.

Sangnawakij, P., & Anlamlert, W. (2023). Alternative confidence interval for variability parameters in the normal distribution with applications to stock exchange index data set. Austrian Journal of Statistics, 52(5), 63-81. https://doi.org/10.17713/ajs.v52i5.1534

Sangnawakij, P., & Böhning, D. (2024). On repeated diagnostic testing in screening for a medical condition: How often should the diagnostic test be repeated?. Biometrical Journal, 66(3), 1-16. https://pubmed.ncbi.nlm.nih.gov/38637326/

Sankaran, M. (1970). The discrete Poisson-Lindley distribution. Biometrics, 26, 145-149. https://doi.org/10.2307/2529053

Sen, S., Maiti, S. S., & Chandra, N. (2016). The xgamma distribution: statistical properties and application. Journal of Modern Applied Statistical Methods, 15(1), Article 38.

Shanker, R. (2016). The discrete Poisson-Amarendra distribution. International Journal of Statistical Distributions and Applications, 2(2), 14-21. https://doi.org/10.11648/j.ijsd.20160202.11

Shanker, R., & Fesshaye, H. (2015). On Poisson-Lindley distribution and its applications to biological sciences. Biometrics & Biostatistics International Journal, 2(4), 103-107. https://doi.org/10.15406/bbij.2015.02.00036

Shanker, R., Fesshaye, H., Shanker, R., Leonida, T. A., & Sium, S. (2017). On discrete Poisson-Shanker distribution and its applications. Biometrics & Biostatistics International Journal, 5(1), Article 00121. https://doi.org/10.15406/bbij.2017.05.00121

Shukla, K. K., & Shanker, R. (2019). A discrete Poisson-Ishita distribution and its applications. International Journal of Statistics and Economics, 20(2), 109-122. https://doi.org/10.15406/bbij.2017.05.00121

Tang, W., He, H., & Tu, X. M. (2023). Applied categorical and count data analysis. Chapman and Hall/CRC.

Weems, K. S., Sellers, K. F., & Li, T. (2023). A flexible bivariate distribution for count data expressing data dispersion. Communications in Statistics - Theory and Methods, 52(13), 4692-4718. https://doi.org/10.1080/03610926.2021.1999474

Wilcox, R. R. (2011). Introduction to robust estimation and hypothesis testing. Academic press.