Multinomial logistic regression analysis of breast cancer
Keywords:
multinomial logistic regression(MLR), logistic regression, classification, predictionAbstract
This study aims at developing Multinomial Logistic Regression (MLR) to evaluate the probability of breast cancer, proposing MLR to predict five stages of breast cancer (Benign, I, II, III and IV). Nine characteristics of breast cancer: Clump Thickness (X1); Uniformity of Cell Size (X2); Uniformity of Cell Shape (X3); Marginal Adhesion (X4); Single Epithelial Cell Size (X5); Bare Nuclei (X6); Bland Chromatin (X7); Normal Nucleoli (X8); and Mitoses (X9) are used as independent variables. Results show that Multinomial Logistic Regression (MLR) yields a coefficient of a model indicating that X1 and X6 have significance less than 0.05. Thus, the prediction of log – likelihood function for a classification staging of breast cancer with P(Y£4) of stage IV is a reference category, reducing a model as:
This study aims at developing Multinomial Logistic Regression (MLR) to evaluate the probability of breast cancer, proposing MLR to predict five stages of breast cancer (Benign, I, II, III and IV). Nine characteristics of breast cancer: Clump Thickness (X1); Uniformity of Cell Size (X2); Uniformity of Cell Shape (X3); Marginal Adhesion (X4); Single Epithelial Cell Size (X5); Bare Nuclei (X6); Bland Chromatin (X7); Normal Nucleoli (X8); and Mitoses (X9) are used as independent variables. Results show that Multinomial Logistic Regression (MLR) yields a coefficient of a model indicating that X1 and X6 have significance less than 0.05. Thus, the prediction of log – likelihood function for a classification staging of breast cancer with P(Y£4) of stage IV is a reference category, reducing a model as:
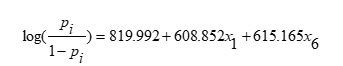
References
Agreti, A. (2002). Categorical Data Analysis, (2nd ed.). New York, USA: John Wiley & Sons.
Bandhita, P. & Noparat, T. (2006, June). Ordinal Regression Analysis in factors related to Sensorial Hearing Loss of the Employee. Industrial factory in Lampang Thailand. Mathematic, Statistics and Their Application, Penang.
Hayatshahi, S. H. S., Abdolmaleki, A., Safarian, S., & Khajeh, K. (2005, October). Non-linear quantitative structure-activity relationship for adenine derivatives as competitive inhibitors of adenosine deaminase. Biochem Biophys Research Comunication., 338, 1137-1142. Retrieved from http://elsevier.com/locate/ybbrc.
Hosmer, D. W. & Lemeshow, S.(2000). Application of logistic regression. New York, USA: John Wiley & Sons.
Jobson , J. D. (1992). Applied multivariate data analysis, (2nd ed.). New York, USA/ Berlin Heidelberg: Springer.
Long, J. S. (1997). Regression Models for categorical and Limited Dependent Variables, USA: Sage Publication, Inc.
Stephenson, B. (2008). Chapter 3 Binary response and logistic regression analysis. Retrieved from http:// public.iastate.edu/~stat415/stephenson/
Swets, J. (1988). Measuring the accuracy of diagnostic systems. Science, 240, 1285-1293.
doi : 101126/science.3287615
Swets, J. A., Dawes, R. M. & Monahan, J. (2000, October). Better decisions through science. Scientific American, 283, 82-87.
Vecchio, T (1966). Predictive value of a single diagnostic test in unselected populations. New England Journal of Medicine, 274, 1171-1173.
Wingo, P.A., Tong, T. & Bolden, S. (1995). Cancer statistics, CA Cancer J Clin, 46(1), 5-27. doi : 10.3322/canjclin.46.1.5
Downloads
Published
How to Cite
Issue
Section
License

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.






