Free Vibration Analysis of Orthotropic Thick Plates by Boundary Element Method
Keywords:
Analog Equation Method, Boundary Element Method, Free Vibration of Orthotropic Thick PlatesAbstract
Background and Objectives: A study of free vibration of shear deformable orthotropic plates holds significant importance and interest in various aspects. Understanding the vibration behavior of these plates enhances the design of stronger and more stable structures, reducing the risk of damage or structural failure over time. Study of the behavior of orthotropic plates, with their directional mechanical properties, are crucial for selecting efficient materials for specific structural applications, such as in aerospace and high-rise buildings. The application of orthotropic plates extends across advanced technologies in industries like automotive, aerospace, and electronics. Additionally, the insights gained from vibration analysis would facilitate the optimization of structural designs, minimizing unwanted vibrations and enhancing load-bearing capabilities. The boundary element method is known for its high efficiency and accuracy in solving complex engineering problems, making it an ideal choice for such analysis. The present study aimed to apply the boundary element method to investigate the free vibration behavior of thick orthotropic plates under general boundary conditions and shapes.
Methodology: The present analysis is based on Mindlin's theory of moderately thick plates and formulates the equations of motion using the Hamilton's principle. The proposed approach employs the principle of the analog equation to determine the frequencies and mode shapes for free vibration analysis of the plates. This technique involves substituting the original problem's equations of motion with three Poisson equations under fictitious forces that conform to the original boundary conditions. These fictitious forces are computed using the boundary element method and approximated using radial basis functions.
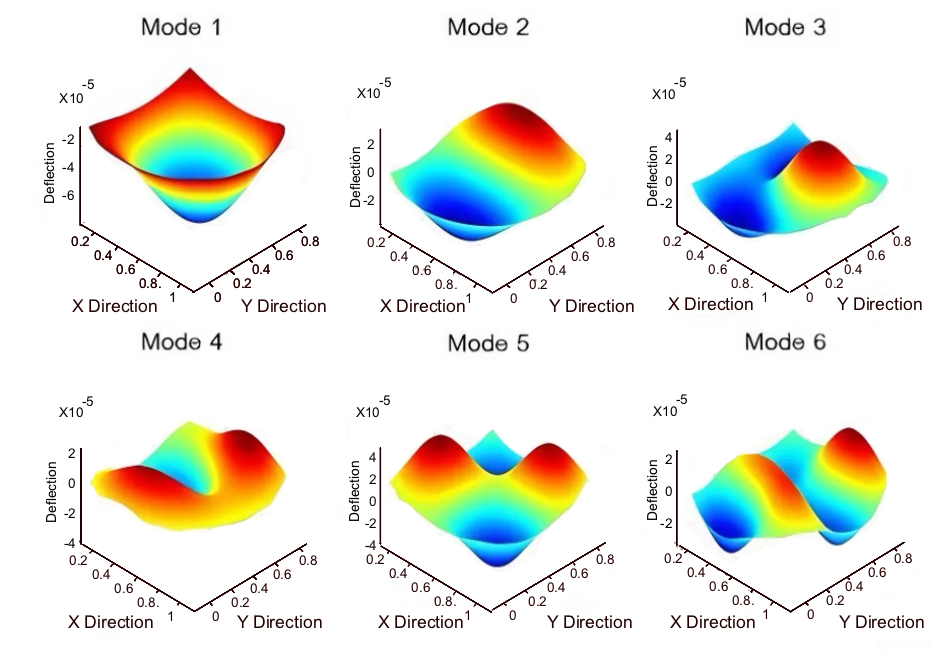
Main Results: To validate the reliability and accuracy of the method, the analysis results were compared with those of other research. The results show that the error for the first vibrational mode ranges from 0.035% to 1.236%. Additionally, the convergence of the solution reveals that the optimal number of boundary elements ranges from 160 to 240, while the number of internal nodes within the domain ranges from 196 to 400. The proposed methodology could effectively analyze the natural frequencies and mode shapes of orthotropic thick plates with general boundary conditions, ranging between elastic support and elastic restraint. Furthermore, this research investigated the parameters affecting the free vibration of orthotropic thick plates. The efficiency of the proposed method is demonstrated by analyzing the free vibration of orthotropic thick plates with complex shapes and boundary conditions. The analysis shows that the natural frequencies are in good agreement with those obtained using other solutions, demonstrating the effectiveness of the boundary element method employing the principle of the analog equation. The method is capable of accurately depicting the vibration behavior of complex-shaped orthotropic thick plates.
Conclusions: The solutions obtained from the boundary element method are consistent with those from previous research, indicating its suitability for analyzing free vibration problems of orthotropic thick plates. The present study highlights the robustness and precision of the boundary element method in handling complex geometries and boundary conditions, making it a valuable tool for structural engineers. The ability to efficiently and accurately investigate natural frequencies and mode shapes ensures its practical applicability in the design and analysis of advanced structural systems. Future work could expand on this research by exploring the effects of different material properties and boundary conditions, as well as extending the method to analyze forced vibrations.
Practical Application: The proposed method can efficiently analyze natural frequencies and mode shapes of complex-shaped orthotropic thick plates under general boundary conditions for use in designing plate structures.
References
Biancolini, M., Brutti, C. and Reccia, L., 2005, “Approximate Solution for Free Vibrations of Thin Orthotropic Rectangular Plates,” Journal of Sound and Vibration, 288 (1–2), pp. 321–344.
Demasi, L., 2006, “Quasi-3D Analysis of Free Vibration of Anisotropic Plates,” Composite Structures, 74 (4), pp. 449–457.
Xing, Y. and Liu, B., 2009, “New Exact Solutions for Free Vibrations of Thin Orthotropic Rectangular Plates,” Composite Structures, 89 (4), pp. 567–574.
Liu, X., Wang, Q. and Quek, S.T., 2002, “Analytical Solution for Free Vibration of Piezoelectric Coupled Moderately Thick Circular Plates,” International Journal of Solids and Structures, 39, pp. 2129–2151.
Shafiee, A., Alizadeh, Y. and Redekop, D., 2003 “Free Vibration of Completely Free Coupled Orthotropic Rectangular Plates,” Journal of Sound and Vibration, 267, pp. 366-370.
Karami, G. Malekzadeh, P. and Mohebpour, S.R., 2006, “DQM Free Vibration Analysis of Moderately Thick Symmetric Laminated Plates with Elastically Restrained Edges,” Composite Structures, 74, pp. 115–125.
Chinnaboon, B., Chucheepsakul, S. and Katsikadelis, J. T., 2011, “A BEM-Based Domain Meshless Method for The Analysis of Mindlin Plates with General Boundary Condition,” Computer Methods in Applied Mechanics and Engineering, 200, pp. 1379-1388.
Hosseini-Hashemi, S., Fadaee, M. and Rokni Damavandi Taher, H., 2011, “Exact Solutions for Free Flexural Vibration of Lévy-type Rectangular Thick Plates Via Third-order Shear Deformation Plate Theory,” Applied Mathematical Modelling, 35 (2), pp. 708–727.
Thai, H.T. and Kim, S.E, 2012, “Levy-type Solution for Free Vibration Analysis of Orthotropic Plates Based on Two Variable Refined Plate Theory,” Applied Mathematical Modelling, 36 (8), pp. 3870–3882.
Senjanovic´, I., Vladimir, N. and Tomic´, M., 2013, “An advanced Theory of Moderately Thick Plate Vibrations,” Journal of Sound and Vibration, 332, 1868–1880.
Petrolito, J., 2014, “Vibration and Stability Analysis of Thick Orthotropic Plates Using Hybrid-Trefftz Elements,” Applied Mathematical Modelling, 38, pp. 5858-5869.
Ye, T., Jin, G., Su, Z. and Chen, Y., 2014, “A Modified Fourier Solution for Vibration Analysis of Moderately Thick Laminated Plates with General Boundary Restraints and Internal Line Supports,” International Journal of Mechanical Sciences, 80, pp. 29-46.
Wang, Q., Shi, D. and Shi, X., 2015, “A Modified Solution for The Free Vibration Analysis of Moderately Thick Orthotropic Rectangular Plates with General Boundary Conditions, Internal Line Supports and Resting on Elastic Foundation,” Meccanica, pp. 1-33.
Wang, Q., Shi, D., Liang, Q. and e Ahad, F., 2016, “A Unified Solution for Free In-plane Vibration of Orthotropic Circular, Annular and Sector Plates with General Boundary Conditions,” Applied Mathematical Modelling, 40 (21–22), pp. 9228-9253.
Pang, F., Li, H., Miao, X. and Wang, X., 2017, “A Modified Fourier Solution for Vibration Analysis of Moderately Thick Laminated Annular Sector Plates with General Boundary Conditions, Internal Radial Line and Circumferential Arc Supports,” Curved and Layered Structures, 4 (1), pp. 189-220.
Ghashochi-Bargh, H. and. Razavi, S., 2018, “A Simple Analytical Model for Free Vibration of Orthotropic and Functionally Graded Rectangular Plates,” Alexandria Engineering Journal, 57, pp. 595-607
Jeeradit, S., 2021, Analysis of Thick Orthotropic Auxetic Plates by Boundary Element Method, Master of Engineering Thesis, Civil Engineering, Faculty of Engineering, King Mongkut's University of Technology Thonburi, 135 p. (In Thai)
Katsikadelis, J.T., 2014, The Boundary Element Method for Plate Analysis: BEM for Dynamic Analysis of Plates, Elsevier Science Inc., Oxford, pp. 217-220.
Zheng, X., Xu, D., Ni, Z., Zhou, C., An, D., Wang, B. and Li, R., 2021, “New Benchmark Free Vibration Solutions of Non-Lévy-type Thick Rectangular Plates Based on Third-order Shear Deformation Theory,” Composite Structures, 268, pp. 113955.
Eftekhari, S.A. and Jafari, A.A., 2013, “Modified Mixed Ritz-DQ Formulation for Free Vibration of Thick Rectangular and Skew Plates with General Boundary Conditions,” Applied Mathematical Modelling, 37 (12–13), pp. 7398–7426.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 King Mongkut's University of Technology Thonburi

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Any form of contents contained in an article published in Science and Engineering Connect, including text, equations, formula, tables, figures and other forms of illustrations are copyrights of King Mongkut's University of Technology Thonburi. Reproduction of these contents in any format for commercial purpose requires a prior written consent of the Editor of the Journal.





